লিওনার্দো ফিবোনাচ্চি – মধ্যযুগে ইউরোপের অন্যতম শ্রেষ্ঠ গণিতবিদ হিসেবে তাঁকে আখ্যা দেওয়া হয়। তিনি তাঁর লিবার আবাকি নামক গ্রন্থে ইউরোপে গণিতচর্চার সূচনা করেন। এই গ্রন্থের মাধ্য়মেই ইউরোপ শূন্য় সংখ্য়াটি সম্বন্ধে অবগত হয়। এই গ্রন্থে তিনি রাশিমালার কথা লেখেন যার প্রামানিক তথ্য প্রকৃতিতে প্রচুর পরিমানে পাওয়া যায়। এই রাশিমালায় এমন এক অনুক্রমের সূত্র পাওয়া যায় যাকে ফিবোনাচ্চি সিকোয়েন্স বা অনুক্রম বলা হয়। এটি শুরু হয় ২টি প্রাথমিক পূর্বনিবিষ্ঠ দ্বিনিধানি (default binary) সংখ্যা ০ ও ১ দিয়ে।তার পর ধারার প্রত্যেকটা সংখ্যা হয় তার আগের দুটি সংখ্যার যোগফলের সমান।
অতএব ফিবোনাচ্চি অনুক্রম হল: ০, ১, ১, ২, ৩, ৫, ৮, ১৩, ২১, ৩৪, ৫৫, ৮৯, ১৪৪…. (অসীম) পর্যন্ত যেকোনো সংখ্যা।এটি একটি অসীম সিকোয়েন্স বা ধারা। একে Fn দ্বারা প্রকাশ করা হয়ে থাকে। এই অনুক্রম আমাদের চারিপাশে বিরাজমান, ফুল, পাতা, ফল, গাছপালা, পশুপাখি, পোকামাকড়, সমুদ্রের ঢেউ এর বাঁক এমনকি অন্তরীক্ষের আকাশগঙ্গার চক্রেও দৃশ্যমান। এমনকি মৌমাছির বংশধারাও সম্পূর্ণরূপে ফিবনাচ্চি সিকোয়েন্স দ্বারা নিয়ন্ত্রিত।
এবার আসি, ফিবনাচ্চি নিজের গ্রন্থে আর কি লিখেছিলেন, তাঁর লিবার আবাকি গ্রন্থটির একটি জায়গায় আমরা পাই
“I loved Indian Mathematics to such an extent above all others that I completely devoted myself to it”
(আমি ভারতীয় গণিত এতটাই ভাালোবাসি যে তাতেই জীবন সমর্পণ করেছি।)
“I was also introduced to Greek, Arabic & Egyptian Math”
(আমি গ্রীক, আরবী এবং মিশরীয় গণিতও অধ্য়য়ন করেছি।)
“But I found ALL of them, EVEN Pythagoras, to be erroneous compared to Indian Mathematics”
(কিন্তু ভারতীয় গণিতের সামনে তারা সবাই, এমনকি পীথাগোরাসও ভ্রান্ত বলেই মনে হয়।)
এবং কোত্থাও তিনি লেখেননি যে অনুক্রম টি তিনি নিজে আবিষ্কার করেছেন। শুধু বিশ্বের দরবারে এই আশ্চর্য গাণিতিক আবিষ্কারটি তুলে ধরেছেন মাত্র।
“For this reason, basing my book completely on Indian methods and applying myself with greatest attention to it, but not without adding something of my own thought, I forced myself to compose this book.”
(এই কারণে আমার বইটি সম্পূর্ণভাবে ভারতীয় গণিতের পদ্ধতির প্রতি সমর্পিত হল…)
তবে কে ছিলেন এই অনুক্রমটির আবিষ্কারক?
এক সময় ভারতীয় গণিতশাস্ত্রের মান এত উন্নত ছিল যে দেশ বিদেশের গণিতজ্ঞরা এদেশে শিক্ষা নিতে উদ্গ্রীব ছিলেন। আর্যভট্ট, ভাস্করাচার্য্য, বৌদ্ধায়ন, বরাহমিহির, শ্রীধর, ব্রহ্মগুপ্ত, হেমচন্দ্র, মহাবীর .. এনারা ছিলেন প্রাক ইসলামিক যুগের বিখ্যাত গণিতজ্ঞ। তাঁদের হাত ধরেই প্রাচীন ভারতীয় গণিতের ইতিহাসের স্বর্ণ যুগের সুচনা হয়। তেমনি এক বিখ্যাত গণিতজ্ঞ ছিলেন পিঙ্গল|
তাঁর রচিত ছন্দ সূত্রের অষ্টম অধ্যায়ে “রূপে শূন্যম” এবং “দ্বি-শূন্যে” সূত্র বিশ্লেষণ করলে দেখা যায় যে একটি বিশেষ ধরনের ছন্দ দিয়ে তিনি একটি সমাহার (combination) গঠন করেছেন। একেই ছন্দ শাস্ত্র বা ছন্দ সূত্র বলা হয়। ছন্দের মাত্রায় লঘু এবং গুরু স্বরের সাথে কোনো মাত্রার সংহত ছন্দের ক্রম প্রতিটি পাদে কত রকম হতে পারে অর্থাৎ তার সমাহার ও বিন্যাস কি কি হতে পারে তা মহামুনি পিঙ্গলের ছন্দ শাস্ত্রে লিপিবদ্ধ আছে। এই ছন্দ গুলি কাব্যাকারে লিপিবদ্ধ হওয়াতে বেশ শ্রুতিমধুর। বৈদিক যুগে রচিত যে কোন শাস্ত্র, মহাকাব্য সবই এই ছন্দাকারে লিপিবদ্ধ। অবিশুদ্ধ গাণিতিক বিচারধারাকে কাব্যাকারে লিপিবদ্ধ করার পেছনেও সেই একই ভূমিকা পালন হয়। পরবর্তী কালে এই শাস্ত্রের আধুনিক সংস্করণ হয় প্রায় ২০০০ বছর পর ইউরোপে, বর্তমানে কালে আমরা যাকে “পাস্কাল-ত্রিভুজ” বলে মানি।
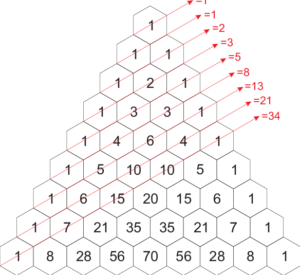
মহামুনি পিঙ্গল এবং ফিবোনাচ্চি ধারার মধ্যে মিল কোথায়? হিন্দু সভ্যতার কেন্দ্রবিন্দু এককালে ছিল মেরু পর্বত। মহামুনি পিঙ্গল তাঁর এই ছন্দবিন্যাসকে নাম দিয়েছিল মাত্রা মেরু। এটি অগনিত সংখ্যা নিয়ে গঠিত একটি পিরামিড, যেখানে তির্যকভাবে একটি কাল্পনিক রেখা টানলে একটি অনুক্রম পাওয়া যায় {১,১,২,৩,৫,৮,….} যেটি আজ “পাস্কাল-ত্রিভুজ” নামে পরিচিত এবং তার মধ্যে একটি অনুক্রম পাওয়া যায় যাকে ফিবোনাচ্চি অনুক্রম বলা হয়। এই ফিবোনাচ্চি অনুক্রমের সমীকরণ উৎপন্ন হয় fn = { f(n-1)+f(n-2)}|
এ থেকে আরো প্রমানিত হয় যে মাত্রামেরুর ব্যবহার ফিবোনাচ্চি অনুক্রমের সূত্রপাতের ২০০০ বছরেরও আগে থেকেই ছিল এবং শুধু গণিতজ্ঞরাই নন কবিরাও তার অনুসরণ করতেন। এই মাত্রামেরু আজো আমাদের দেশে নানান রুপে ব্যবহৃত হয়, যেমন হিন্দুস্তানি ও কর্ণাটকি সঙ্গীতে। তা নিয়ে যদিও আলোচনা করতে গেলে আরো একখানি অধ্যায় হয়ে যাবে।
প্রাচীন সভ্যতাগুলির মধ্যে এক অনন্য অসাধারন বিদ্যাচর্চায় লিপ্ত ছিল আমাদের ভারতীয় সভ্যতা। গণিতচর্চা।
বৈদিক যুগের ঋষিদের গভীর জ্ঞান-সঞ্জাত দার্শনিক উচ্চারণে আমরা শূন্যের কথা দেখতে পাই। এই শূন্য অবশ্যই গণিতের শূন্য-সংখ্যা নয়, কিন্তু শূন্যতার বোধকে এই সভ্যতা দার্শনিক ভাবে থেকে অত্যন্ত সহজে এবং কৌতুহলের সাথে গ্রহণ করেছিল। ঋকবেদের নাসদীয় সুক্ত, বৌদ্ধ মহাযানের মাধ্যমক শৈলীর শূন্যবাদী দর্শন, তন্ত্রের নিরাকার নিষ্কল শিবের ধারণা, নৈয়ায়িকের অভাব বোধ – সর্বত্র গণিতচর্চা, তার দার্শনিকগত প্রভাব এবং বিশ্লেষণের প্রমান দেয়। বেদাঙ্গ জ্যোতিষে গণিতকে তুলনা করা হয়েছিল নাগের মাথার মণির সাথে, ময়ূরের মাথার শিখার সাথে।

